9759. ABB

Фернандо был нанят Университетом Ватерлоо для завершения недавно начатого проекта. Университет планирует за пределами кампуса построить представительную улицу с бунгало для важных иностранных гостей и сотрудников.

В настоящее время улица застроена лишь частично: она начинается у берега озера и тянется к лесу, где и заканчивается. Задача Фернандо — завершить застройку улицы, построив ещё несколько бунгало в её конце, у леса. Все уже построенные дома расположены на одной стороне улицы, и новые бунгало должны быть размещены на той же стороне. Существующие бунгало различаются по типу и окрашены в разные цвета.

На взгляд Фернандо, улица выглядит немного хаотично. Он опасается, что новые дома, выполненные по его собственному дизайну, только усилят это впечатление. Чтобы внести элемент порядка, он решил подобрать такие цвета для новых бунгало, чтобы вся цветовая последовательность домов на улице стала симметричной. Это означает, что последовательность цветов должна читаться одинаково с обоих концов улицы.

Среди прочих задач Фернандо интересует, какое минимальное количество новых бунгало необходимо построить и покрасить соответствующим образом, чтобы завершить проект в соответствии с задуманной симметрией.

Вход. В первой строке задано целое число n (1 ≤ n ≤ 4 * 10⁵) – количество уже построенных бунгало.

Во второй строке дана последовательность их цветов в порядке от начала улицы у озера. Это строка длиной n, состоящая из строчных латинских букв от ‘a’ до ‘z’, каждая из которых обозначает определённый цвет.

Выход. Выведите минимальное количество бунгало, которые нужно добавить в конец улицы и покрасить соответствующим образом, чтобы вся цветовая последовательность стала симметричной.

Пример входа 1	Пример выхода 1
3 abb	1

Пример входа 2	Пример выхода 2
12 recakjenecep	11

РЕШЕНИЕ

z-функции

Анализ алгоритма

К данной строке необходимо добавить минимальное количество символов, чтобы она стала палиндромом. Для этого нужно найти наибольший палиндром среди всех её суффиксов, затем взять префикс до начала этого палиндрома, развернуть его и приписать к исходной строке.

Например, наибольшим палиндромным суффиксом строки abcxqx является xqx. Префикс до него – abc, переворачиваем его (получаем cba) и приписываем к исходной строке.

Рассмотрим строку rs = reverse(s) + s. Вычислим для нее z-функцию.

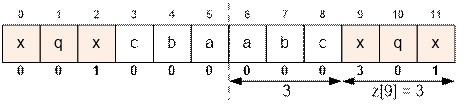
Найдём наименьший индекс i (такой, что i ≥ n), для которого выполняется равенство i + z[i] = 2n. При этом значение z[i] будет максимальным среди таких индексов. Минимальное количество символов, которое необходимо дописать к исходной строке, чтобы получить палиндром, равно n – z[i].

Для строки “abcxqx” (длина n = 6) нужный индекс i = 9, так как 9 + z[9] = 9 + 3 = 12 = 2 * 6.

Пример

Рассмотрим первый пример. Вычислим z-функцию для строки reverse(s) + s = “bba” + “abb” = “bbaabb”.

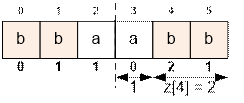
Наименьшим индексом i (i ≥ n), для которого выполняется равенство i + z[i] = 2n, является i = 4. Действительно: 4 + z[4] = 4 + 2 = 6 = 2 * 3. Тогда ответ равен n – z[i] = 3 – 2 = 1. То есть, к строке “abb” достаточно добавить один символ ‘a’, чтобы получить палиндром “abba”.

Реализация алгоритма

Функция z строит и возвращает z-функцию для строки s.

vector<int> zfun(string s)

{

int i, l, r, len = s.size();

vector<int> z(len, 0);

l = r = 0;

for (i = 1; i < len; i++)

{

if (i <= r) z[i] = min(r - i + 1, z[i - l]);

while (i + z[i] < len && s[z[i]] == s[i + z[i]]) z[i]++;

if (i + z[i] - 1 > r)

{

l = i;

r = i + z[i] - 1;

}

}

return z;

}

Основная часть программы. Читаем входную строку s.

cin >> n;

cin >> s;

Строим строку rs = reverse(s) + s.

rs = s;

reverse(rs.begin(), rs.end());

rs += s;

Вычисляем z-функцию строки rs.

z = zfun(rs);

Находим наименьший индекс i (i ≥ n), для которого выполняется равенство i + z[i] = 2n. Среди всех таких индексов значение z[i] будет наибольшим.

for (i = n; i < rs.size(); i++)

if (i + z[i] == 2 * n)

{

Выводим ответ.

cout << n - z[i] << endl;

break;

}